Spatial Averaging#

Updated: 02/29/24 [xcdat v0.6.1]

Overview#

A common data reduction in geophysical sciences is to produce spatial averages. Spatial averaging functionality in xcdat allows users to quickly produce area-weighted spatial averages for selected regions (or full dataset domains).

In the example below, we demonstrate the opening of a (remote) dataset and spatial averaging over the global, tropical, and Niño 3.4 domains.

The data used in this example is pulled directly from the Earth System Grid Federation (ESGF).

Users can install their own instance of xcdat and follow these examples using their own environment (e.g., with vscode, Jupyter, Spyder, iPython) or enable xcdat with existing JupyterHub instances. The conda environment used in this notebook includes xcdat, xesmf, matplotlib, ipython, ipykernel, cartopy, and jupyter:

conda create -n xcdat_notebook -c conda-forge xcdat xesmf matplotlib ipython ipykernel cartopy nc-time-axis jupyter

2. Global average#

[2]:

# if you do not specify lat_bounds or lon_bounds, the averager will calculate the domain mean
ds_global_avg = ds.spatial.average("tas")

[3]:

ds_global_avg.tas

[3]:

<xarray.DataArray 'tas' (time: 1980)> Size: 16kB
array([12.52127071, 13.09115223, 13.60703132, ..., 15.5767848 ,
       14.65664621, 13.84951678])
Coordinates:
    height   float64 8B 2.0
  * time     (time) object 16kB 1850-01-16 12:00:00 ... 2014-12-16 12:00:00

[4]:

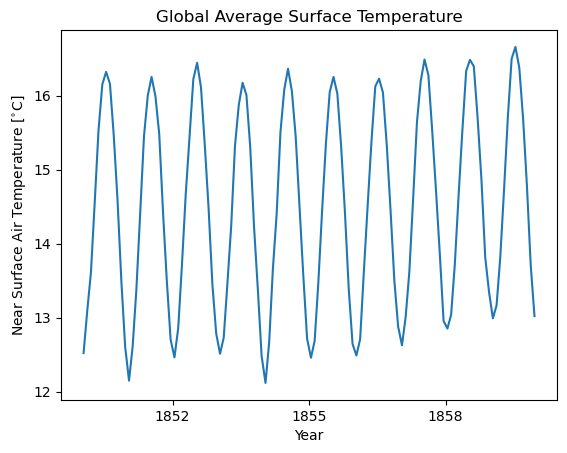
# Plot the first 120 time steps
ds_global_avg.tas.isel(time=slice(0, 120)).plot()
plt.title("Global Average Surface Temperature")
plt.xlabel("Year")
plt.ylabel("Near Surface Air Temperature [$^{\\circ}$C]")

[4]:

Text(0, 0.5, 'Near Surface Air Temperature [$^{\\circ}$C]')

../_images/examples_spatial-average_7_1.png

3. Tropical average#

[5]:

# compute the tropical average
ds_trop_avg = ds.spatial.average("tas", lat_bounds=(-25, 25))

[6]:

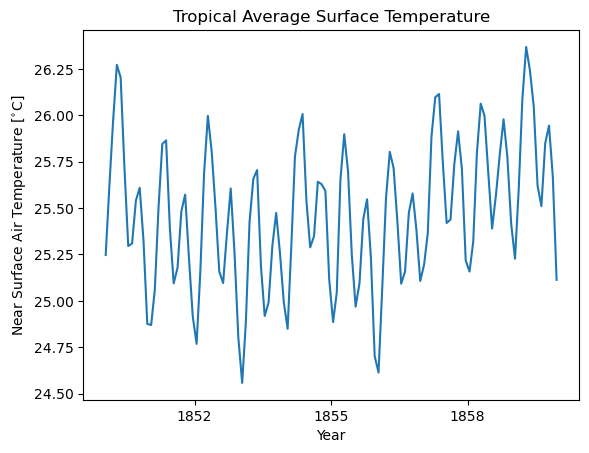
# Plot the first 120 time steps
ds_trop_avg.tas.isel(time=slice(0, 120)).plot()
plt.title("Tropical Average Surface Temperature")
plt.xlabel("Year")
plt.ylabel("Near Surface Air Temperature [$^{\\circ}$C]")

[6]:

Text(0, 0.5, 'Near Surface Air Temperature [$^{\\circ}$C]')

../_images/examples_spatial-average_10_1.png

4. Nino 3.4 Region#

Niño 3.4 (5N-5S, 170W-120W): The Niño 3.4 anomalies may be thought of as representing the average equatorial SSTs across the Pacific from about the dateline to the South American coast. The Niño 3.4 index typically uses a 5-month running mean, and El Niño or La Niña events are defined when the Niño 3.4 SSTs exceed +/- 0.4C for a period of six months or more.”

—https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni

[7]:

# compute the nino 3.4 average
ds_nino_avg = ds.spatial.average("tas", lat_bounds=(-5, 5), lon_bounds=(190, 240))

[8]:

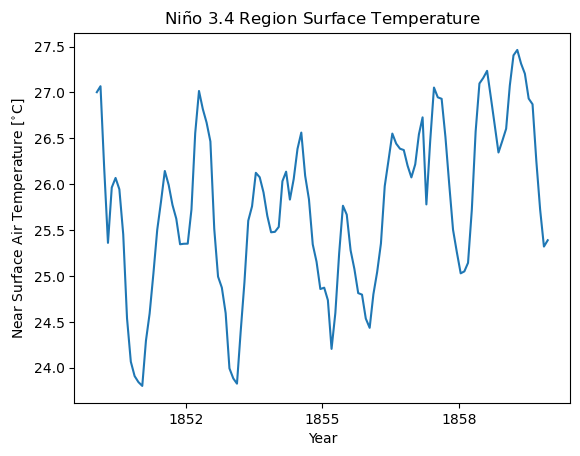
# Plot the first 120 time steps
ds_nino_avg.tas.isel(time=slice(0, 120)).plot()
plt.title("Ni$\\mathrm{\\tilde{n}}$o 3.4 Region Surface Temperature")
plt.xlabel("Year")
plt.ylabel("Near Surface Air Temperature [$^{\\circ}$C]")

[8]:

Text(0, 0.5, 'Near Surface Air Temperature [$^{\\circ}$C]')

../_images/examples_spatial-average_13_1.png

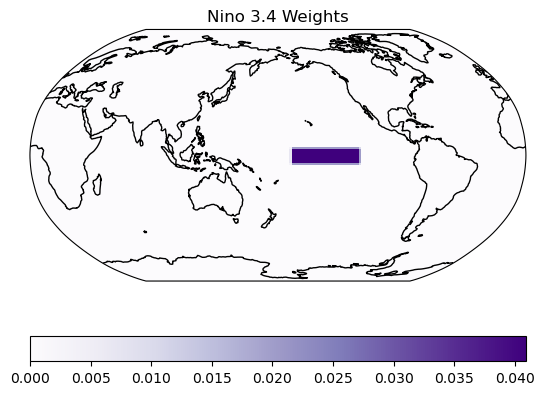
5. Retain / Inspect Spatial Weights#

xCDAT can retain the weights used for spatial averaging using keep_weights=True. Here we retain and inspect these weights for the Niño 3.4 region. Note that along the edges of the Niño 3.4 box the weights are slightly less (since some grid cells are not fully in the averaging box and thus receive partial weight).

[9]:

# recompute the nino 3.4 average, but retain weights
ds_nino_avg = ds.spatial.average(
    "tas", lat_bounds=(-5, 5), lon_bounds=(190, 240), keep_weights=True
)

[10]:

# plot the weights
ax = plt.axes(projection=ccrs.Robinson(central_longitude=180.0))
plt.pcolor(
    ds_nino_avg.lon,
    ds_nino_avg.lat,
    ds_nino_avg.lat_lon_wts.T,
    transform=ccrs.PlateCarree(),
    cmap=plt.cm.Purples,
)
ax.coastlines()
plt.colorbar(orientation="horizontal")
plt.title("Nino 3.4 Weights")

[10]:

Text(0.5, 1.0, 'Nino 3.4 Weights')

../_images/examples_spatial-average_16_1.png

6. Create and apply your own weights#

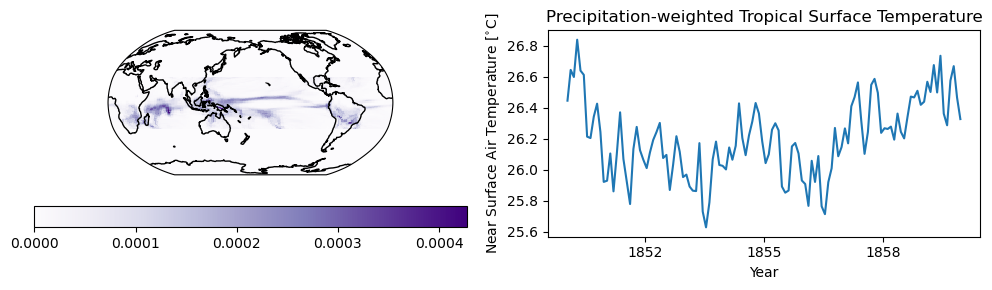
Instead of having xcdat generate geospatial weights, you may want to create your own weights. You can pass your own weights into xcdat. Here we show an example of weighting the surface temperature data in the tropics by precipitation.

Warning: The lat_bounds and lon_bounds args are used when calculating axis weights, but is ignored if weights are supplied.

[11]:

# let's grab and open the precipitation dataset that corresponds to our temperature data
filepath = "https://esgf-data1.llnl.gov/thredds/dodsC/css03_data/CMIP6/CMIP/CSIRO/ACCESS-ESM1-5/historical/r10i1p1f1/Amon/pr/gn/v20200605/pr_Amon_ACCESS-ESM1-5_historical_r10i1p1f1_gn_185001-201412.nc"
ds_pr = xc.open_dataset(filepath)

[12]:

# we will use the precip data as weights (zeroing out extratropical data)
weights = ds_pr.pr.where(np.abs(ds_pr.pr.lat) < 30, 0.0)
# and apply a cos(lat) weighting
weights = weights * np.cos(np.radians(ds_pr.lat))
# compute precipitation weighted temperature
ds_pw = ds.spatial.average("tas", weights=weights)

[13]:

# plot the first timestep of the weights matrix
plt.figure(figsize=(10, 3))
ax = plt.subplot(1, 2, 1, projection=ccrs.Robinson(central_longitude=180.0))
plt.pcolor(
    ds_pr.lon, ds_pr.lat, weights[0], transform=ccrs.PlateCarree(), cmap=plt.cm.Purples
)
ax.coastlines()
plt.colorbar(orientation="horizontal", ticks=[0, 0.0001, 0.0002, 0.0003, 0.0004])
plt.subplot(1, 2, 2)
plt.title("Weights (time=")

# plot the first 120 time steps
ds_pw.tas[0:120].plot()
plt.title("Precipitation-weighted Tropical Surface Temperature")
plt.xlabel("Year")
plt.ylabel("Near Surface Air Temperature [$^{\\circ}$C]")
plt.tight_layout()

../_images/examples_spatial-average_20_0.png

7. Compute a zonal average#

You do not need to average over both latitude and longitude. Here we show an example in which we take the zonal average (average over all longitude values).

[14]:

# take zonal average
ds_zonal = ds.spatial.average("tas", axis=["X"])

[15]:

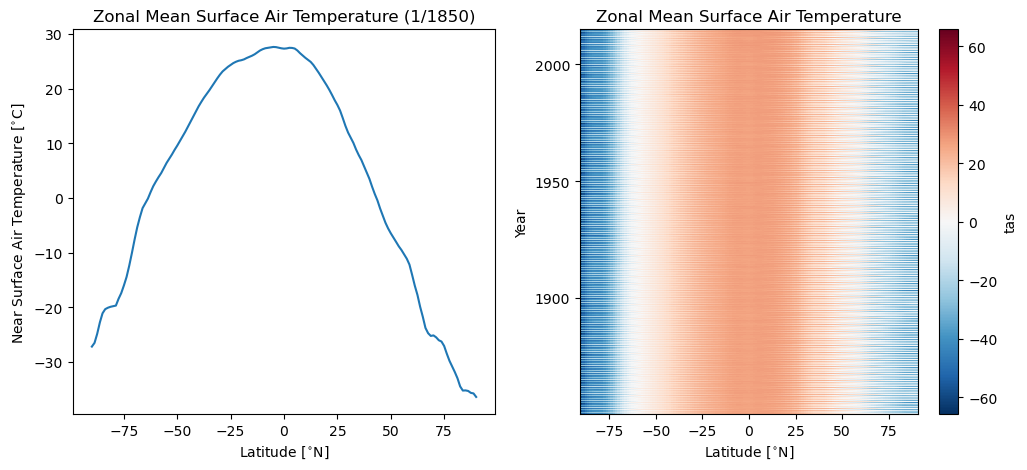
# plot first time step
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
ds_zonal.tas[0].plot()
plt.ylabel("Near Surface Air Temperature [$^{\\circ}$C]")
plt.xlabel("Latitude [$^{\\circ}$N]")
plt.title("Zonal Mean Surface Air Temperature (1/1850)")

# plot hovmoller
plt.subplot(1, 2, 2)
ds_zonal.tas.plot()
plt.xlabel("Latitude [$^{\\circ}$N]")
plt.ylabel("Year")
plt.title("Zonal Mean Surface Air Temperature")

[15]:

Text(0.5, 1.0, 'Zonal Mean Surface Air Temperature')

../_images/examples_spatial-average_23_1.png

Spatial Averaging

Contents

Spatial Averaging#

Overview#

1. Open the `Dataset`#

2. Global average#

3. Tropical average#

4. Nino 3.4 Region#

5. Retain / Inspect Spatial Weights#

6. Create and apply your own weights#

7. Compute a zonal average#

Spatial Averaging

Contents

Spatial Averaging#

Overview#

1. Open the Dataset#

2. Global average#

3. Tropical average#

4. Nino 3.4 Region#

5. Retain / Inspect Spatial Weights#

6. Create and apply your own weights#

7. Compute a zonal average#

1. Open the `Dataset`#